Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- 하이라이트 테이블
- explicit random effect model
- 토스 data assistant
- 모수추정
- 태블로
- 백준 알고리즘 기초1
- 토스 sql
- 덤벨차트
- 계산된 필드 만들기
- wishart parameter 추정법
- toss sql
- 단어뒤집기
- Tableau
- 코테select
- 스타벅스 워드클라우드
- 카테고리와 메뉴명을 한 번에 살펴보기
- 범례 워크시트 위 이동
- 태블로부트캠프
- 조세퍼스 문제
- 당분 함유량과 칼로리의 상관관계
- wishart laplace transform
- wishart gamma random effect model
- sql코테준비
- d similar
- torch.nn.Linear
- adp필기문제
- 시/군/구 별 매장 분포 현황
- 메뉴명 별 칼로리 & 카페인
- d similar matrices class
- adp문제
Archives
- Today
- Total
수리통계 분석 코딩 실습
[Bayesian] 베이지안 가설 검정 - 고전적 검정 본문
✔ 베이지안 검정과 대비되는 고전적 검정의 한계를 알아보자
0. 귀무가설, 대립가설이란?
1. 고전적 검정
2. 고전적 가설 검정의 중요도
3. 고전적 가설 검정의 단점
0. 귀무가설, 대립가설이란?
예를 들어, 귀무가설로는 갈릴레오 갈릴레이의 '지구는 둥글다'라는 가설을 입증할때, 보편적으로 사람들이
믿었던 내용인 '지구는 네모낳다'가 귀무가설($H_0$)가 되는 것이며,
갈릴레오 갈릴레이의 '지구는 둥글다'가 대립가설($H_1$)이 된다.
귀무가설이란
보편적으로 받아드려지는 사실을 말함.
대립가설이란
입증하고자 하는 사실을 말함.
1. 고전적 검정
❗❗ 고전적 검정의 기본 BASE
고전적 검정은 항상 $H_0$ 즉, 귀무가설을 중심으로 검정이 이뤄진다.
다시말해, 귀무가설이 사실일때 기각되지 않도록 보수적으로 검정이 진행됨.
검정의 결과는 $H_0$를 기각하거나 $H_0$를 기각하지 않거나 둘 중의 하나를 뜻함.
이때, 검정은 $X \sim f(x|\theta)$일때, 관측치 ($x_1, \cdots, x_n$)에 의존함.

▷ 검정 오류
- 1종 오류 : $H_0$가 사실이 아닐때, $H_0$를 기각하는 오류
- 2종 오류 : $H_0$가 사실이 아닐때, $H_0$를 받아드리는 오류
- 기각역 C: $H_0$를기각하도록 하는 ($x_1,\cdots,x_n$ )의 영역
2. 고전적 가설 검정의 중요도
1종오류 >>> 2종 오류
즉, 잘못된 $H_0$를 받아드릴 지 언정, 사실인 $H_0$를 기각하지 않도록 검정을 해야함
→ 채택 방식
1종 오류 확률의 상한가(유의수준 $\alpha$)를 정하고, 2종 오류를 작게 만드는 기각역 C 선택
→ 유의 확률을 이용한 검정
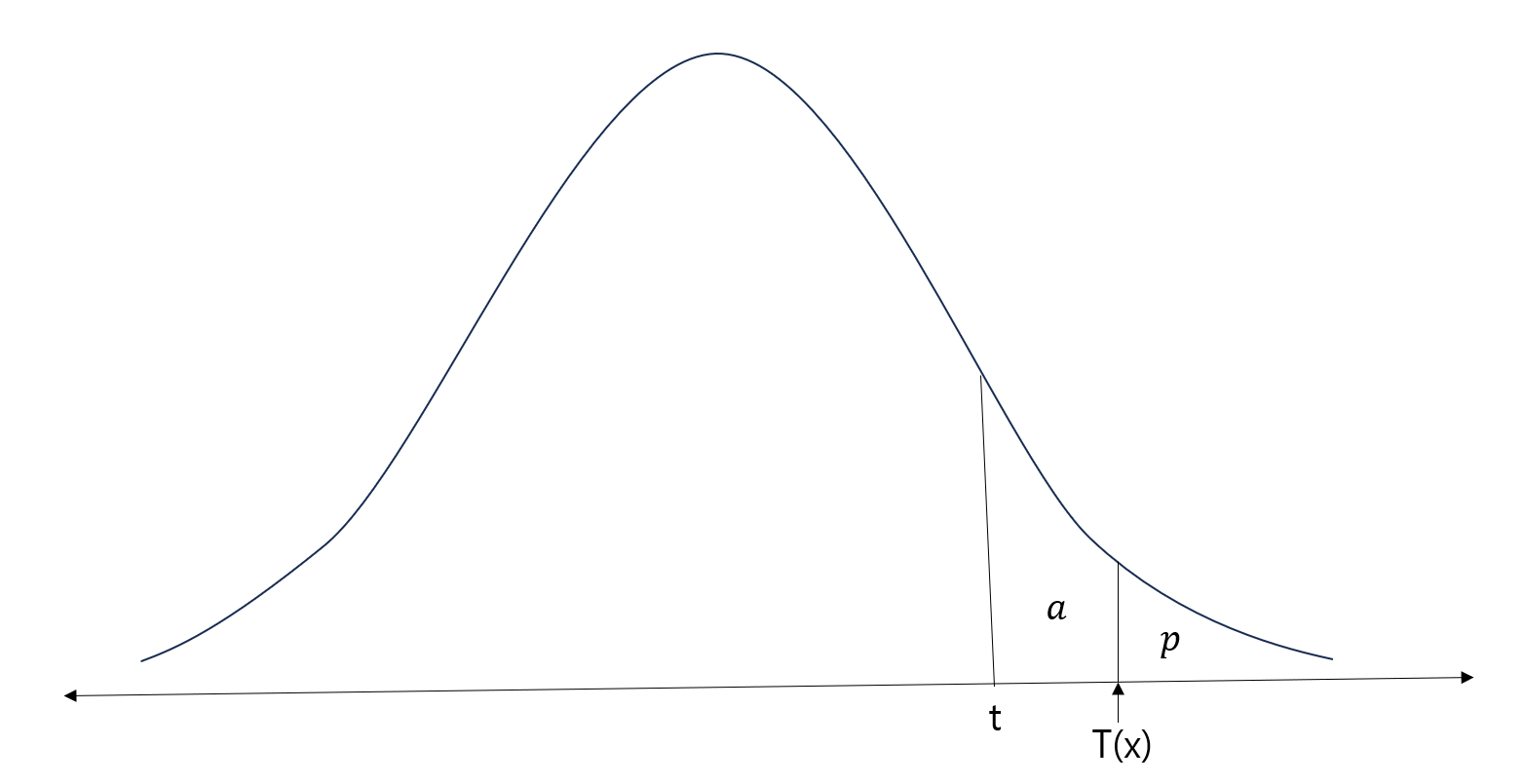
※ 검정통계량 T = T(X)
- 유의 확률(p) = T가 관측값 t=T(X)와 같거나 더 극단적인( 대립가설 방향으로 가는 것 )값을 가질 확률
- 유의 확률(p) < 유의수준($\alpha$) ☞ $H_0$ 기각
3. 고전적 가설 검정의 단점
- $H_0$가 $H_1$에 nested된 경우가 아니면 적용이 어려움
예) H0: 성장곡선이 이차곡선이다 vs H1: 성장곡선이 지수함수곡선이다 - 유의확률이 관측값 뿐만 아니라 관측되지 않은 '더 극단적인 값'에도 의존함
$H_1: \mu > 0$ 이면, 보편적인 사실인 $H_0: \mu = 0$임. 그러므로, $\mu > 0$라는 것은,
추출은 한번만 이뤄져 하나의 표본에 대해선 관측되지 않은 값을 마치 여러번 표본을 뽑아, 관측한 것처럼
더 극단적인 값(대립가설에 치우져치도록)에도 의존하게 됨. - 귀무가설과 대립가설의 구분이 검정에 영향을 끼침
고전적인 방법하에선, $H_0$는 특정값을 지니고, 귀무가설과 대립가설을 구분해야 하는데, 이 구분 자체가 위험성을 지닐 때가 있음.
예) $H_0: \rho = 1$ vs $H_1: -1 < \rho <1$로 두면, 귀무가설은 보수적이고, 위험하지 않은 값을 지녀야 하는데, $\rho$가 1인, 특정값을 갖게 되면, 자기 상관계수가 매우 높음으로 분석하게 되어 매우 위험한 분석 결과를 초래함.

